Ordonnancement

1 Généralités

On se propose d'atteindre un objectif dont la réalisation suppose l'exécution de plusieurs tâches soumises à diverses contraintes.

1.1 L'Ordonnancement d'un projet c'est:

1) Déterminer l'ordre et un calendrier d'exécution des diverses taches compatibles avec les contraintes de façon à minimiser un critère, le plus souvent le temps global de réalisation du projet.

2) Repérer les éléments critiques du projet (qui ne peuvent être ralentis sans retarder l'ensemble du projet).

3) Améliorer le projet en:

Ø Allongeant des taches non critiques (diminution du coût).

Ø Diminuer des taches critiques (accélération au meilleur coût).

Ø Intégrer de nouvelles contraintes.

Les problèmes d'ordonnancement se rencontrent dans de nombreux domaines: La construction et les travaux publics, la gestion de la production et l'organisation d'ateliers, la gestion de projet (en particulier de projets informatiques), la conception de systèmes d'exploitation multi-tâches en informatique, etc....

2 Formalisation.

Nous allons définir des notions dans le cas d'un problème où

1) L'ensemble des tâches est connu de manière statique et n'évolue pas avec le déroulement du projet.

2) L'exécution d'une tâche ne peut pas être interrompue (tâche non morcelable),

2.1 Les tâches

Soit n le nombre de tâches, numérotées 1, 2, ... , i, ..., n .

Notations:

dd_i = date de début de la tâche i

df_i = date de fin de la tâche i

d_i = durée d'exécution de la tâche i

Si l'exécution de la tâche i ne peut pas être interrompue, on obtient: df_i=dd_i+d_i

L'ordonnancement est alors totalement défini par les dates de début des tâches.

A une tâche i sont souvent associées deux dates extrêmes:

a_i = date de disponibilité de la tâche i

b_i = date d'échéance ou de livraison de la tâche i

Un ordonnancement réalisable devra vérifier les contraintes: a_i £ dd_i £ df_i £ b_i

2.2 Les contraintes

2.2.1 Relations entre les tâches

Les tâches peuvent être liées par des relations d'antériorité. Souvent, elles se réduisent à des relations de succession simple:

"Pour commencer la tâche k , la tâche i doit être terminée"

La succession simple se traduit ici par dd_k ³ df_i ou de préférence : dd_k - dd_i ³ d_i

On dit simple par opposition à la contrainte suivante:

"Pour commencer la tâche k , la tâche i doit être commencée depuis 3 unités de temps"

qui se traduit ici par dd_k ³ dd_i + 3 ou de préférence : dd_k - dd_i ³ 3

De telles contraintes sont appelées contraintes potentielles, leur forme général est:

dd_k - dd_i ³ d(i, k)

où d(i, k) est un nombre quelconque (positif ou non), dont la signification dépendra de la situation concernée.

On se limitera dans un premier temps, à des contraintes potentielles correspondant à des relations de succession simple. Le cas général sera étudié ensuite.

2.2.2 Les ressources

La réalisation des tâches nécessitent l'emploi de ressources spécifiques. Leur limitation à chaque instant conduit à ce que l'on appelle les contraintes cumulatives.

La disponibilité des ressources peut être constante au cours du temps, ou bien évoluer, généralement selon un échéancier connu. On distinguera deux cas:

1) Les ressources renouvelables:

Les ressources utilisées par l'exécution d'une tâche redeviennent disponibles dès que la tâche est terminée: Les machines, la main d'œuvre sont des ressources renouvelables.

2) Les ressources consommables

Elles disparaissent avec l'exécution de la tâche à laquelle elles sont allouées: Les ressources monétaires (financement des tâches), les matières premières sont des ressources consommables.

2.3 Les critères (d'optimisation)

Le critère le plus souvent utilisé consiste à minimiser la durée totale, c'est à dire la date de la fin des travaux.

On peut aussi chercher à minimiser une fonction économique dépendant des retards pris par l'exécution des tâches par rapport aux dates d'échéance. Par exemple, avec les notations précédentes, le retard de la tâche i s'écrit: R_i = Max( df_i - b_i , 0 )

Minimiser le plus grand retard = Max { R_i ; i=1 ... n }

Minimiser la somme des retards = R_i

Minimiser une somme pondérée des retards = c_i R_i

Minimiser un coût calculé en fonction de l'utilisation des ressources nécessaires aux tâches.

3 Modélisation du problème

On dispose de 2 représentations graphiques possibles élaborées vers la fin des années 1950:

Ø Méthode PERT (Program Evaluation Research Task) (mis au point par la NASA dans le cadre de la construction des fusées Polaris).

Ø Méthode MPM (Méthode Potentiel Metra) par B. Roy.

Dans les 2 cas on doit :

Ø décomposer le projet en tâches de durées connues.

Ø répertorier les antériorités

Ø répertorier les autres contraintes.

Un exemple:

Taches	A	B	C	D	E	F	G	H
Durées	12	7	6	5	4	7	15	4
Antécédents			A,B	A,B	B	C,D	A,E	D,E

Ce tableau se lit, par exemple: La tâche C ne peut commencer que si les tâches A et B sont terminées et elle dure 6 unités de temps.

3.1 Graphe MPM.

Aussi appelé Graphe Potentiel Tâche ou AON (Activity on Node).

On construit un graphe valué orienté G(X,U), aussi appelé graphe potentiel taches en associant à chaque tache i un sommet X_i de X et à chaque contrainte potentielle écrite sous la forme: dd_k - dd_i ³ a(i,k) un arc (X_i, X_k) de valeur a(i,k) qui on le verra peut même être négative.

On ajoute aussi un sommet "début" et un sommet "fin", repères des dates de début et de fin des travaux.

Exemple

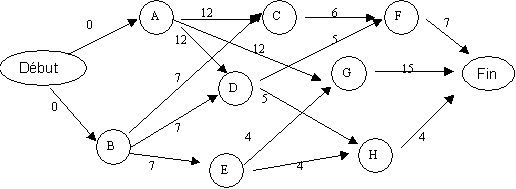
Ici il n'y a que des contraintes de succession simple, les arcs sortants d'un sommet ont donc tous la même longueur (a(i,k) = di pour tout k).

Le sommet "début" est avant le début de toutes les tâches et le sommet "fin" après la fin de toutes les tâches. Par souci de clarté on se contente d'attacher ces sommets par des arcs non déduisibles (par exemple "début"èC est inutile puisque C est après la fin de A).

3.2 Graphe Pert.

Aussi appelé Graphe Potentiel Etape ou AOA (Activity on Arc).

On construit un graphe valué orienté G = ( X , U ) tel que:

Les sommets correspondent maintenant à des étapes "après la fin des tâches antérieures " et "avant le début des tâches suivantes". On doit encore ajouter une étape "début" et une étape "fin".

Les arcs représentent

Soient des tâches réelles (chaque tâche est représentée par un arc de valeur la durée de celle-ci).

Soient des tâches fictives. Ces dernières ont pour objet de représenter des antériorités. Les tâches fictives sont également valuées. On notera a(i, k) la valeur d'un arc fictif reliant les étapes i et k. Pour le moment on pose a(i, k) = 0.

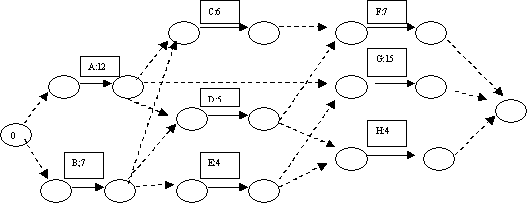
Le graphe P.E.R.T. correspondant à l'exemple ci-dessus est :

-Version 1 –

On remarque qu'il y a beaucoup d'arcs et de sommets. Il est possible d'envisager d'autres représentations, celle-ci a pour elle de proposer une solution systématique (graphe totalement développé).

- Version 2 -

3.2.1 Remarques

Un problème d'ordonnancement peut-être représenté par plusieurs graphes PERT. Le graphe PERT comporte plus de sommets et d'arcs que le graphe Potentiels - Tâches, mais permet une visualisation des étapes de fin des tâches et, de ce fait, une meilleure compréhension des marges. Le graphe totalement développé est en fait très proche du graphe MPM.

Quand on réduit un graphe PERT, il faut faire attention de ne pas perdre d'informations. Un procédé de vérification demande d'énumérer pour chaque tache la liste des taches antécédentes (en sautant les taches fictives).

Le résultat doit être conforme au problème posé. Ici les tâches antécédentes de G sont: E, A, B.

L'hypothèse ne parle que de A et E mais il n'y a pas contradiction puisque l'on sait par ailleurs que B est avant E.

3.3 Propriétés du graphe associé.

Dans les deux cas, on a associé au problème d'ordonnancement un graphe orienté dont les arcs sont porteurs d'informations sur la durée des tâches et les relations de précédence entre celles-ci.

Définition. On appelle ordonnancement réalisable un système de dates dt(X) associées aux sommets X du graphe (représentant les tâches ou les étapes du problème) et vérifiant:

Pour tout arc (Xi, Xj) : dt(Xj) - dt(Xi) ³ d(i, j), d(i, j) étant la longueur de l'arc (Xi, Xj) :

On fixe une origine du temps en posant arbitrairement dt("début") = 0.

Proprièté: Pour tout chemin C allant du sommet "début" du projet à un sommet donné X_i , et pour tout ordonnancement, on a:
dt(X_i) ³ longueur du chemin C

En effet, soit un chemin C = { Début, X₁ , X₂ , ... , X_i }

Les contraintes potentielles correspondantes s'écrivent:

dt(X₁) - dt(Début) ³ d(Début, X₁)

dt(X₂) - dt(X₁) ³ d(X₁, X₂)

…….

dt(X_i-1) - dt(Xi-2) ³ d(X_i-2, Xi_-1)

dt(X_i) - dt(X_i-1) ³ d(Xi_-1, Xi)

D'où, en faisant la somme des inégalités:

dt(X_i) = dt(X_i) - dt("Début") ³ = longueur du chemin C

Donc la date d'un sommet du graphe (date d'une étape) est donc supérieure ou égale à la longueur du plus long chemin allant du sommet début des travaux au sommet considéré.

Rappel: Le problème admet des ordonnancements réalisables si et seulement si le graphe associé ne comporte aucun circuit de longueur strictement positive.

4 Le problème central de l'ordonnancement.

4.1 Méthode du chemin critique.

Les seules contraintes prises en compte sont les contraintes potentielles (contraintes de succession) et l'on cherche à proposer un jeu de dates aux sommets qui minimise la durée totale du projet.

La fonction critère est donc minimiser (date(Fin) - date(Début)) = minimiser (date(Fin)).

4.2 Ordonnancement au plus tôt des étapes.

En prenant comme date, pour chaque étape, la longueur du plus long chemin allant du "début" des travaux à l'étape considérée, on obtient un ordonnancement réalisable particulier, appelé ordonnancement au plus tôt.

Un plus long chemin allant du début à la fin des travaux est appelé le chemin critique. Sa longueur, qui est la date au plus tôt du sommet fin des travaux, est la durée totale minimum compatible avec les contraintes d'antériorité.

Les tâches de ces chemins critiques sont les tâches critiques: Tout retard dans leur réalisation (donc toute augmentation de leur durée) est intégralement répercuté sur la durée totale minimum.

Pour des problèmes ne présentant que contraintes potentielles de succession simples (ce que nous envisageons pour le moment) on peut donc utiliser l'algorithme de Bellman.

Il faut cependant savoir que dans le cas général le graphe peut présenter des circuits et imposer l'utilisation de l'algorithme de Ford

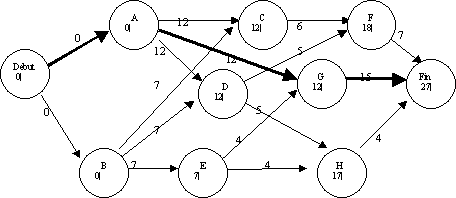
Cas de notre exemple: la durée totale minimum est de 27 et les tâches critiques sont A et G.

4.3 Ordonnancement au plus tard des étapes.

La durée totale minimum étant connue grâce au calcul des dates au plus tôt, on peut se demander quel retard peuvent prendre les tâches non critiques sans augmenter la durée totale minimum (les tâches critiques ne pouvant prendre aucun retard).

Il suffit de déterminer, pour chaque sommet, le plus long chemin allant de ce sommet à la fin des travaux: la date au plus tard est alors égale à la durée totale minimum (déjà calculée avec les dates au plus tôt) moins cette longueur.

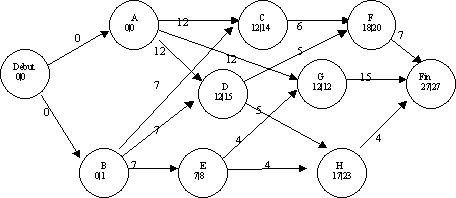
Il peut aussi sembler plus simple de considérer le graphe obtenu en inversant le sens de tous les arcs et en calculant la longueur des plus longs chemins allant de la fin des travaux (devenue la racine du graphe) à chaque sommet.

4.3.1 Cas du graphe PERT:

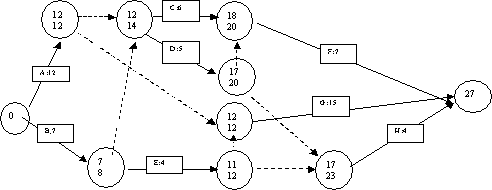
On procède de la même façon. Pour l'exemple précédent, on obtient les dates au plus tôt et au plus tard suivantes:

Attention aux dates associées aux sommets. Si (X, Y) est un arc encadrant une tâche A, tôt(X) est la date au plus tôt du début de A, tard(Y) est la date au plus tard de la fin de A.

4.4 Les marges.

En appelant tôt(X) (resp tard(X)) la date au plus tôt (resp. tard) de la tâche X, on voit qu'une date dt(X) de début de X compatible avec la durée totale des travaux doit vérifier tôt(X) <= dt(X)<= tard(X).

Cependant retarder le début de X n'est peut-être pas sans conséquences sur le début des autres tâches.

4.4.1 Marge totale:

C'est le retard maximum que l'on peut imposer au début d'une tâche sans modifier la durée totale du projet: (Les marges totales des tâches critiques sont toujours nulles).

Dans le cas du graphe MPM :Mt(i) = tard(i) - tôt(i).

Dans le cas du graphe PERT: Sa tache i de durée d(i) est encadrée par les étapes X(i), Y(i):

c'est Mt(i) = tard(Y(i))-tôt(X(i))-d(i)

Exemple Mt(E) = 12 - 7 - 4 = 1.

4.4.2 Marge libre:

Elle représente le retard maximum que l'on peut imposer au début d'une tâche sans modifier les dates au plus tôt des tâches suivantes.

Pour la tâche i, on a Ml(i) = min(tôt(z)/ z successeur de i) - tôt(x(i)) - d(i).

Exemple Ml(E) = 11 - 7 - 4 = 0.

Remarque: Tache critique èMarge totale = 0 è Marge libre = 0.

5 Diagramme de Gantt.

Offre une visualisation différente d'un ordonnancement en représentant les taches par une bande horizontal dont la position est fixée sur l'axe des abscisse par les dates de début et de fin.

On obtient donc des diagrammes différents selon que l'on utilise un ordonnancement au plus tôt, au plus tard, ou intermédiaire:

Pour l'exemple traité plus haut dans le cours associé à un ordonnancement au plus tôt, on obtient:

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27
A
B
C
D
E
F
G
H

6 Contraintes de ressources

6.1 Ressources renouvelables

Une ressource est dite renouvelable si son utilisation pour la réalisation d'une tâche la laisse à nouveau disponible une fois la tâche terminée.

Exemple: les équipements ou la main d'œuvre. (par opposition aux matières premières qui sont consommées par la tâche).

6.1.1 Courbe de charge

On associe au diagramme de Gantt un diagramme montrant le cumul des ressources utilisées au même moment. Exemple:

Avec une demande de ressource de 7 pour A, 4 pour B, 3 pour C et de 6 pour D.

Diagramme de Gantt associé aux dates au plus tôt:

On en déduit la courbe de charge associée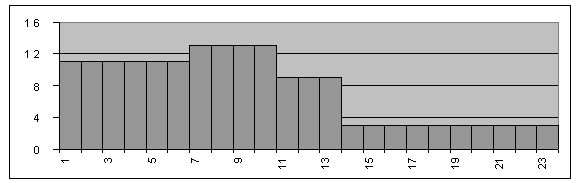

Diagramme de Gantt associé aux dates au plus tard:

On en déduit la courbe de charge associée

6.2 Ressources non renouvelables: Algorithme du décalage

On considère le problème:

Tâches	A	B	C	D
Durées	7	8	6	9
Antécédents	-	-	A , B	B
Coûts	7	7	7	7

Pour lequel on a un financement par tranches de 10 aux dates 0, 5 et 10.

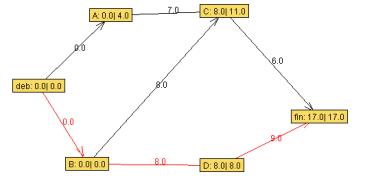
On trace sur un même graphe la courbe des besoins cumulés et celle des ressources cumulées

L'ordonnancement est réalisable si à tout moment la courbe des ressources excède celle des besoins.

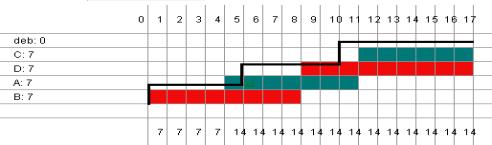
On peut noter que cette condition n'est pas satisfaite dans notre exemple: Entre les dates 4 et 5 d'une part, et aussi entre les dates 8 et 10.

On recherche alors l'amplitude de la plus longue de ces périodes, ici : 2.

On obtient une solution réalisable en ajoutant +2 à toutes les dates au plus tard: On obtient:

7 Représentation des contraintes générales en MPM

7.1 Principe général

La modélisation des problèmes d'ordonnancement par un graphe de type MPM permet également la gestion de contraintes plus élaborées que les contraintes potentielles d'antériorité simples vues jusqu'à présent.

Le principe général est le suivant:

Un arc (A, B) de valeur dt traduit le fait que deb(B)-deb(A) >= dt.

On se ramène donc systématiquement aux dates de début des tâches, et de se fait il peut apparaître des arcs négatifs et des circuits dans le graphe MPM correspondant.

La recherche des dates au plus tôt et au plus tard peut donc imposer l'utilisation de l'algorithme de Ford.

7.2 Quelques cas

1) Pour commencer la tache B il faut que A (durée da) soit fini depuis au moins dt.

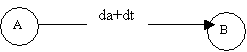
Pour commencer la B il faut que A soit commencée depuis au moins dt.

3) Pour commencer la tâche B il faut que A soit fini depuis au plus dt.

fin(A) +dt >= deb(B) è deb(A) + da + dt >= deb(B) è deb(A)-deb(B) >= -(da+dt)

4) La tâche B doit suivre la tâche A sans délai:

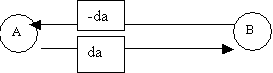
7.3 Exemple de produit en "open source"

Open Workbench: téléchargeable à http://www.openworkbench.org/