Exercices sur les Flots
1.1 Exercice
On considère le réseau de transport suivant:

1) Construire un flot initial admissible et complet.
2) Appliquer l'algorithme de Ford-Fulkerson à ce flot initial pour déterminer le flot maximum.
1.2 Exercice
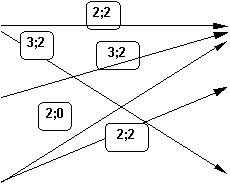
Le société LENOIR est spécialisée dans l'importation de café. Le café acheté par la société est stocké à Santos (4000T) Recife (2000T) et Cartagena (4000T). Il doit être transporté à Moulins via Le Havre, Dunkerque, ou Bordeaux selon le schéma suivant:
![]()
![]()
![]()
![]()
![]()

![]()
![]()
Les valeurs encadrées représentent en premier, les capacités maximales transportables d'une ville à l'autre (en milliers de Tonnes) et en second les valeurs du flot initial (en milliers de Tonnes également).
1) Vérifier qu'il s'agit bien d'un flot. Quelles sont ses propriétés ?
2) Utiliser l'algorithme de Ford-Fulkerson pour déterminer le flot maximal.
3) Préciser une coupe de capacité minimum et la valeur de celle-ci.
Bis:
Le société LENOIR est spécialisée dans l'importation de café. Le café acheté par la société est stocké à Santos (4000T) Recife (2000T) et Cartagena (4000T). Il doit être transporté à Moulins via Le Havre, Dunkerque, ou Bordeaux selon les possibilités suivantes:
Un cargo va de Santos au Le Havre( 2000T max ) et Bordeaux (3000T max).
Un cargo va de Recife au Havre (3000 T max).
Un cargo va de Cartagena au Havre (2000 T max) et Dunkerque (2000 T max).
Des liaisons par véhicules de la société permettent de transporter respectivement
4000T de Le Havre vers Moulins
2000T de Dunkerque vers Moulins
3000T de Bordeaux vers Moulins.
Vérifier que ce problème peut se représenter par un flot.
Utiliser l'algorithme de Ford-Fulkerson pour déterminer le flot maximal.
Préciser une coupe de capacité minimum et la valeur de celle-ci.
1.3 Exercice
On considère le réseau de transport défini par le graphe suivant:

1) Vérifier que les nombres non encadrés forment bien un flot initial compatible avec les capacités.
2) Appliquer la procédure de marquage des sommets de Ford Fulkerson à ce flot initial.
3) En déduire le flot maximum et déterminer une coupe de capacité minimum.
1.4 Exercice
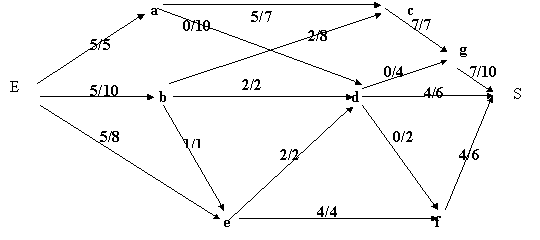
On considère le réseau routier suivant reliant la ville E à la ville S:
![]()
I- On a évalué le nombre maximal de véhicules que chaque route peut écouler par unité de temps, ainsi que la situation actuelle en cas de saturation du réseau.
Ces évaluations en centaines de véhicules sont données sur le graphe précédent.
1) Montrer que le flot actuel est complet.
2) Peut-on améliorer le flot?
3) Si oui rechercher le flot maximum pouvant passer de E à S par unité de temps.
4) Déterminer les arcs de la coupe correspondant au flot maximum.
II- Cette étude a été complétée par l'évaluation du nombre maximal de véhicules pouvant traverser les villes par unité de temps. Ces évaluations en centaines de véhicules sont données dans le tableau ci-dessous:
|
Ville |
a |
b |
c |
d |
e |
f |
g |
|
Débit |
6 |
7 |
8 |
6 |
6 |
5 |
9 |
Après avoir modifié le graphe pour se ramener à un problème de flot maximum déterminer le débit maximal du réseau considéré
1.5 Exercice
Un organisme d'aide sociale dispose de 100 appartements pour loger 100 familles. On a les données suivantes:
|
Nbre de personnes de la famille |
1 |
2 |
3 |
4 |
5 et plus |
|
Nbre de familles |
10 |
13 |
22 |
23 |
32 |
|
Nbre de pièces de l'appartement |
1 |
2 |
3 |
4 |
5 |
|
Nbre d'appartements |
8 |
18 |
20 |
40 |
14 |
On adopte d'autre part les critères de répartition suivants:
Une famille d'une personne peut être logée dans un appartement de 1 ou 2 pièces;
Une famille de 2 personnes peut être logée dans un appartement de 1 ou 2 pièces;
Une famille de 3 personnes peut être logée dans un appartement de 2, 3 ou 4 pièces;
Une famille de 4 personnes peut être logée dans un appartement de 3, 4 ou 5 pièces;
Une famille de 5 personnes ou plus peut être logée dans un appartement de 4 ou 5 pièces;
On veut loger le plus grand nombre possible de familles en respectant ces critères de répartition.
1) Formuler le problème comme un problème de flot sur un réseau que l'on précisera.
2) Une première proposition d'attribution avait conduit aux résultats suivants:
6 appartements d'une pièce attribués à des familles d'une personne,
4 appartements de 2 pièces attribués à des familles d'une personne,
13 appartements de 2 pièces attribués à des familles de 2 personnes,
1 appartement de 2 pièces attribués à une famille de 3 personnes,
20 appartements de 3 pièces attribués à des familles de 3 personnes,
1 appartement de 4 pièces attribué à une famille de 3 personnes,
23 appartements de 4 pièces attribués à des familles de 4 personnes,
16 appartements de 4 pièces attribués à des familles de 5 personnes ou plus,
14 appartements de 5 pièces attribués à des familles de 5 personnes ou plus.
Montrer en appliquant l'algorithme de Ford-Fulkerson à partir de cette solution initiale qu'il est possible de faire mieux.
1.6 Exercice
On considère le réseau de transport suivant où les nombres encadrés associés aux arcs sont les capacités maximales de ceux-ci:
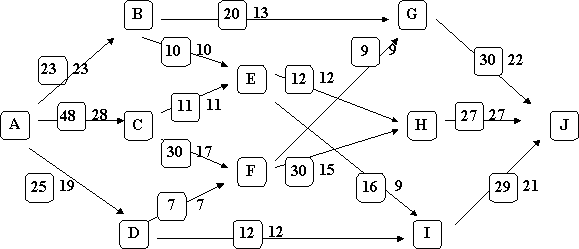
1) Vérifier que les nombres non encadrés forment bien un flot compatible avec les capacités.
2) Calculer la capacité de la coupe définie par les sommets B, E, G, et J.
3) Appliquer l'algorithme de Ford-Fulkerson au flot initial donné jusqu'à obtenir le flot maximum.
4) En déduire une coupe de capacité minimum.
1.7 Exercice
On considère le réseau de transport suivant où les nombres encadrés associés aux arcs sont les capacités maximales de ceux-ci:
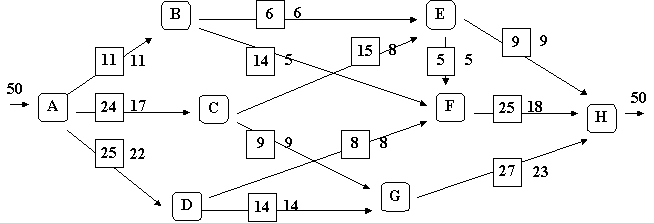
1) Vérifier que les nombres non encadrés forment bien un flot et que ce flot est compatible avec les capacités.
2) Calculer la capacité de la coupe définie par les sommets D, E, G et H.
3) Appliquer l'algorithme de Ford-Fulkerson au flot existant. Montrer que cette algorithme permet
a) de dire que le flot existant n'est pas maximum.
b) de construire une chaîne permettent d'augmenter la valeur du flot sortant du sommet H.
4) Le nouveau flot obtenu en 3) est-il maximum?
Montrer que l'algorithme de Ford-Fulkerson permet alors de construire une coupe de capacité minimum.
1.8 Exercice
On considère le réseau de transport suivant, les nombres encadrés correspondent aux capacités maximum des arcs, les autres valeurs étant celles d'un flot initial proposé.

Appliquer la procédure de marquage jusqu'à obtention du flot maximum.
Déterminer la coupe de capacité minimale.
1.9 Exercice
On considère le réseau de transport suivant (les nombres encadrés étant les capacités maximum des arcs):
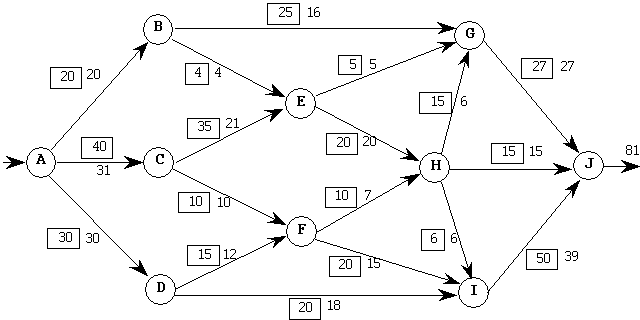 Vérifier que les nombres non encadrés forment bien un flot
initial compatible avec les capacités des arcs.
Vérifier que les nombres non encadrés forment bien un flot
initial compatible avec les capacités des arcs.
Appliquer la procédure de marquage des sommets de Ford-Fulkerson à ce flot initial (on présentera les étapes du marquage à l’aide d’un tableau détaillant les informations nécessaires).
En déduire la chaîne résultant du marquage de la sortie du réseau.
Modifier le flot le long de cette chaîne de manière à augmenter le flot sur l’arc-retour.
Obtenir le flot maximum en réitérant a procédure et déterminer une coupe de capacité minimum.
1.10 Exercice
On considère le réseau de transport suivant, les nombres encadrés correspondant à la capacité maximum des arcs, les autres valeurs étant celles d'un flot initial proposé:
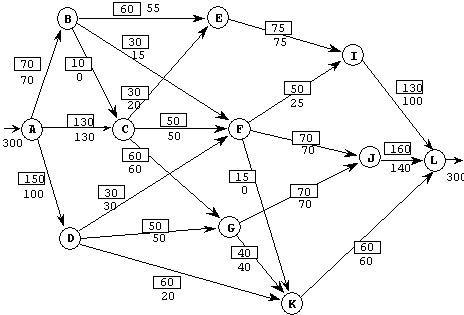
1) Appliquer la procédure de marquage des sommets et en déduire une manière d'améliorer la solution initiale.
2) Déterminer le flot maximum et démontrer son optimalité à l'aide de la coupe de capacité minimum.
1.11 Exercice
La station de sport d'hiver A décide de repenser l'organisation et le rythme de ses remontées mécaniques de façon à permettre au maximum de skieurs d'aller au point L où se trouve un restaurant d'altitude.
Le domaine skiable est alimenté par 16 remontées, dont les capacités maximales et les niveaux d'utilisation aux heures de pointes sont donnés ci-dessous.
Certains départs de remontées sont accessibles directement depuis l'arrivée d'autres remontées, ou bien après une descente en ski plus ou moins longue. Ces trajets en ski sont aussi indiqués et correspondent à des arcs de capacité infinies.
Liste des remontées: capacités et utilisations:
|
arcs |
origine |
extrémité |
capacité maximale |
flot initial |
|
n° 1 |
A |
B |
400 |
370 |
|
n° 2 |
A |
C |
650 |
650 |
|
n° 3 |
A |
D |
750 |
500 |
|
n° 4 |
B |
E |
300 |
275 |
|
n° 5 |
C |
E |
150 |
100 |
|
n° 6 |
C |
F |
250 |
250 |
|
n° 7 |
D |
F |
150 |
150 |
|
n° 8 |
D |
G |
250 |
250 |
|
n° 9 |
D |
K |
300 |
100 |
|
n° 10 |
E |
I |
375 |
375 |
|
n° 11 |
F |
J |
350 |
350 |
|
n° 12 |
F |
K |
100 |
10 |
|
n° 13 |
G |
J |
350 |
350 |
|
n° 14 |
I |
L |
650 |
500 |
|
n° 15 |
J |
L |
800 |
700 |
|
n° 16 |
K |
L |
350 |
320 |
Pistes d'accès à des départs de remontées:
|
Piste |
origine |
extrémité |
|
1 |
B |
C |
|
2 |
B |
F |
|
3 |
F |
I |
|
4 |
C |
G |
|
5 |
G |
K |
1) Tracer le graphe en indiquant les remontées (flèches pleines) et les pistes de transferts (flèches pointillées).
2) En supposant que les chiffres de fréquentation des remontées indiqués correspondent à un flot de transport, en déduire la fréquentation sur les pistes de transfert.
3) Peut-on améliorer ce flot de façon à augmenter la fréquentation du restaurant en L.
On pourra commencer par essayer de saturer les chemins allant directement de A à L).
4) Déterminer les arcs de la coupe de capacité minimale.